Contents
Trọng tâm tam giác là gì?
Trước khi tìm hiểu khái niệm trọng tâm của tam giác, chúng ta cần hiểu rõ đường trung tuyến là gì?
Đường trung tuyến của một tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện.
Từ đó, ta có khái niệm trọng tâm tam giác như sau: Trọng tâm của tam giác chính là giao điểm của 3 đường trung tuyến.
Ví dụ: Cho tam giác ABC với AM, BN, CP lần lượt là 3 đường trung tuyến xuất phát từ 3 đỉnh A, B, C.
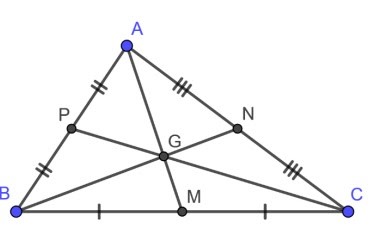
Khi đó, các đường trung tuyến AM, BN, CP cắt nhau tại điểm G. Vì vậy, G chính là trọng tâm của tam giác ABC đã cho.
Trọng tâm tam giác có tính chất gì?
Tính chất của trọng tâm tam giác là: Khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
Giả sử, tam giác ABC có 3 đường trung tuyến là AM, BN, CP với G là trọng tâm như hình. Theo tính chất trên, ta có:
- GA = 2/3 AM
- GB = 2/3 AN
- GC = 2/3 CP

Ngoài ra, chúng ta còn một số hằng đẳng thức khác liên quan đến trọng tâm tam giác. Xét theo khía cạnh, điểm G chia mỗi đường trung tuyến thành 3 phần bằng nhau.
- Đối với đường trung tuyến AM, ta có:
AM = 3 GM; AM = 3/2 AG; AG = 2 GM; GM = 1/2 AG,…
- Đối với đường trung tuyến BN, ta có:
BN = 3 GN; BN = 3/2 BG; BG = 2 GN; GN = 1/2 BG,…
- Đối với đường trung tuyến CP, ta có:
CP = 3 GP; CP = 3/2 CG; CG = 2 GP; GP = 1/2 CG,…
Hướng dẫn chi tiết cách xác định trọng tâm tam giác
Để xác định được trọng tâm của một tam giác, bạn có thể làm theo 2 cách sau:
Cách thứ nhất
- Vẽ tam giác ABC.
- Xác định trung điểm M của cạnh BC sao cho MB = MC.
- Nối A với M để có đường trung tuyến AM.
- Thực hiện tương tự với các cạnh và đỉnh còn lại, bạn sẽ vẽ được thêm 2 đường trung tuyến nữa của tam giác này.
- Gọi giao điểm của 3 đường trung tuyến là điểm G. Khi đó, điểm G chính là trọng tâm tam giác ABC bạn đã vẽ.

Cách thứ hai
- Vẽ tam giác ABC.
- Xác định trung điểm M của cạnh BC sao cho MC = MB.
- Nối đỉnh A với điểm M ta được đường trung tuyến AM.
- Trên đoạn thẳng AM, lấy một điểm G sao cho: AG = 2/3 AM.
- Theo tính chất trọng tâm, điểm G chính là trọng tâm tam giác ABC bạn vừa vẽ.
Trọng tâm tam giác của các hình đặc biệt
Trọng tâm tam giác vuông
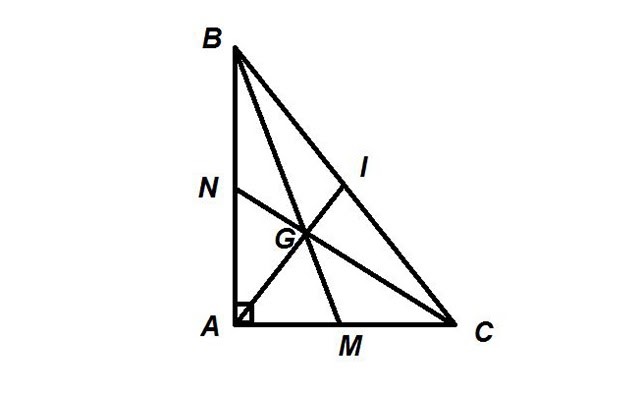
Trọng tâm của tam giác vuông cũng được xác định như tam giác thường.
Xét tam giác ABC vuông tại A với G là trọng tâm. Vì AI là đường trung tuyến của một góc vuông nên ta có: AI = 1/2 BC = BI = CI.
Suy ra, tam giác AIB và tam giác AIC lần lượt cân tại I.
Trọng tâm tam giác cân
Trọng tâm của một tam giác cân cũng được xác định giống tam giác thường.
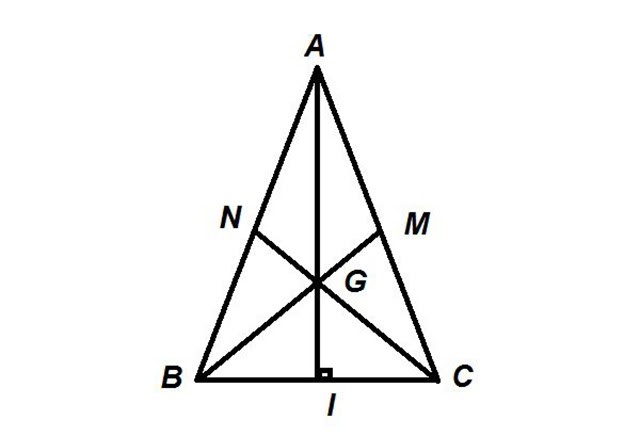
Xét tam giác ABC cân tại A với G là trọng tâm. Khi đó, AG vừa là đường trung tuyến, vừa là đường phân giác và là đường cao của tam giác ABC này.
Ta có: AG vuông góc với BC. Suy ra, tam giác ACI và ABI lần lượt vuông tại I.
Trọng tâm của tam giác vuông cân
Để xác định trọng tâm của tam giác vuông cân, bạn có thể làm theo 2 cách hướng dẫn ở trên.
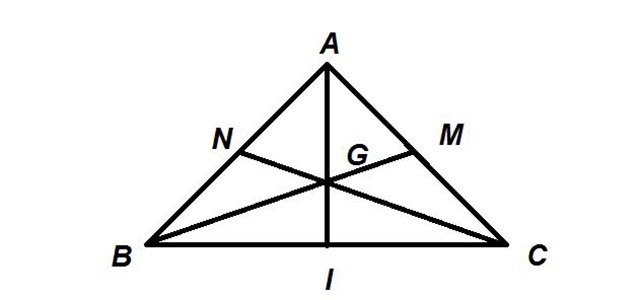
Xét tam giác ABC vuông cân tại A với G là trọng tâm. Tương tự như tam giác cân đã tìm hiểu ở trên, AG là đường trung trực, đường trung tuyến và đường cao của tam giác này. Suy ra, AG vuông góc với BC.
Bên cạnh đó còn có: AB = AC (vì tam giác cân tại A).
Suy ra, BM = CN và BN = AN = CM = AM.
Trọng tâm tam giác đều
Trọng tâm của tam giác đều cũng được xác định theo hướng dẫn ở trên.
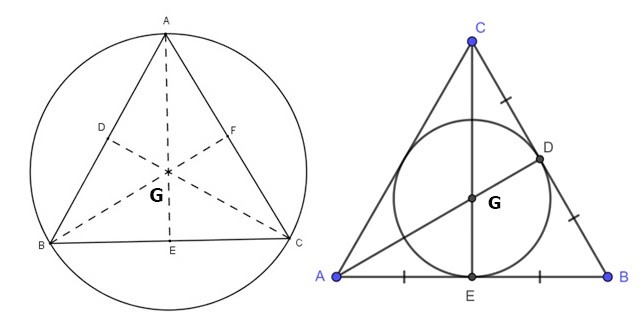
Xét tam giác đều ABC với G là giao điểm của 3 đường trung tuyến xuất phát từ 3 đỉnh. Khi đó, G vừa là trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác đều ABC.
Qua bài viết trên, các bạn đã nhớ lại kiến thức đường trung tuyến, khái niệm trọng tâm tam giác, tính chất và cách xác định trọng tâm rồi đúng không? Trọng tâm của tam giác rất dễ nhầm lẫn với một số điểm khác nên bạn cần chú ý nhé! Mong rằng, những kiến thức trong bài viết sẽ có ích đối với bạn đọc!
Xem thêm:
- Số nguyên là gì? Phân loại, tính chất và cách biểu diễn trên trục số
- Định luật Murphy – Giải đáp tại sao bạn luôn gặp “vận đen”
- Khối lượng riêng là gì? Tổng hợp khối lượng riêng của các chất
- Thế năng đàn hồi là gì? Khái niệm và công thức tính thế năng
- Cường độ điện trường là gì? Các công thức tính cường độ điện trường