Các công thức lượng giác cơ bản đáng nhớ

Công thức lượng giác là một trong những kiến thức quan trọng trong môn toán ở chương trình học của cấp 3. Các công thức lượng giác cơ bản thưởng phải ghi nhớ để áp dụng nhanh trong quá trình làm bài tập. Tuy nhiên không ít bạn cảm thấy các công thức này rất đáng sợ vì vừa dài vừa dễ nhầm lẫn. Nếu các bạn vẫn chưa nhớ hết các công thức lượng giác cơ bản thì hãy dành chút thời gian tham khảo trong bài viết này nhé.

Tìm hiểu công thức lượng giác là gì?

Lượng giác là một từ có nguồn gốc từ tiếng Anh là “Trigonometry” có nghĩa là tam giác + đo lường. Lượng giác là một phần nhỏ trong toán học với mục đích là để tìm hiểu về tình tam giác và mối liên hệ giữa cạnh của tam giác với góc độ của tam giác đó.

Lượng giác có thể chỉ ra hàm số lượng giác. Hàm số lượng giác là đại lượng biểu thị các mối liên kết và có thể áp dụng được vào vật lý để học những hiện tượng có chu kỳ như dao động điều hòa hay sóng âm. 

Công thức lượng giác là gì?

Nhánh toán lượng giác này được phát minh ra từ khoảng thế kỷ thứ 3 trước công nguyên. Ban đầu lượng giác được xem là nhánh toán của hình học và chủ yếu được ứng dụng để nghiên cứu trong lĩnh vực thiên văn. 

Tuy nhiên sau này, lượng giác bắt đầu được mở rộng ra và ứng dụng nhiều hơn, toán đại số, vật lý, hay cả lĩnh vực trắc địa cũng có sự xuất hiện của công thức trong lượng giác.

Các công thức lượng giác trong tam giác vuông

Công thức lượng giác trong tam giác vuông được xem là các công thức cơ bản và dễ nhớ nhất vì nó khá là ngắn và ít. Không để các bạn chờ lâu nữa, chúng tôi sẽ tổng hợp lại các công thức về lượng giác trong tam giác vuông ngay sau đây:

Xét trong một tam giác vuông ABC có góc ở đỉnh A bằng 90 độ. Ta có các công thức cơ bản cần nhớ bao gồm:

AB = BC . sinC = BC . cosB

AC = BC . sin B = BC . cosC

sinB = AC / BC

cosB = AB / BC

tanB = AC / AB

cotB = AB / AC

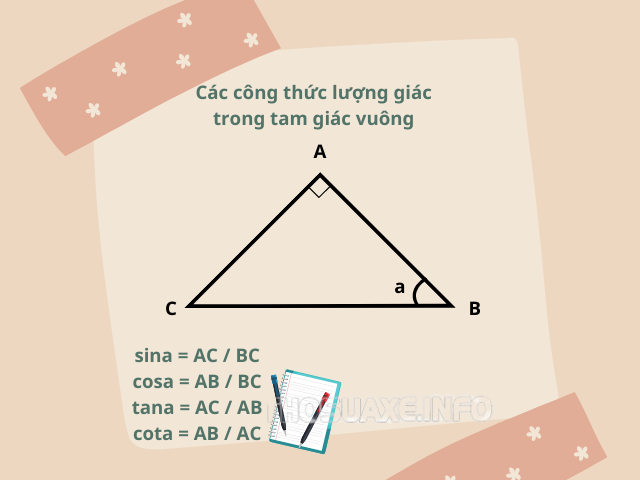
Công thức tính lượng giác trong tam giác vuông ABC

Nếu bạn thấy những công thức như thế này khó để ghi nhớ thì có một mẹo đọc thành văn để dễ dàng thuộc công thức lượng giác trong tam giác vuông hơn đó là: Sin Đi Học – Cos Không Hư – Tan Đoàn Kết – Cot Kết Đoàn. Giả thích ý nghĩa của mẹo này như sau:

Ta có công thức tính sin sẽ bằng cạnh đối chia cạnh huyền (Đ/H – Đi Học); cos bằng cạnh kề chia cạnh huyền (K/H – Không Hư); tan bằng cạnh đối chia cạnh kề (Đ/K – Đoàn Kết); cot bằng cạnh kề chia cạnh đối (K/Đ – Kết Đoàn).

Nhớ các công thức này trong tam giác vuông bằng cách đọc thành văn vần như vậy sẽ giúp các bạn dễ dàng ghi nhớ hơn.

Các công thức lượng giác cơ bản trong toán học

Các công thức cơ bản hay gặp

sin2(a) + cos2(a) = 1

1/ cos2(a) = 1 + tan2(a)

1/sin2(a) = 1 + cot2(a)

tana = sina / cosa

cota = 1 / tana = cosa / sina

Các công thức tính lượng giác cơ bản trong toán học

Công thức cộng

sin(a+b) = sina . cosb + cosa . sinb

sin(a-b) = sina . cosb – cosa . sinb

cos(a+b) = cosa . cosb + sina . sinb

cos(a-b) = cosa . cosb – sina . sinb

tan (a + b) = (tana) + tan(b)) / (1-tanb. tana)

tan (a – b) = (tan(a) – tan(b)) / (1+tanb. tana)

Công thức nhân đôi

sin 2a = 2sina.cosa 

cos 2a = 1 – 2sin2(a) = 2cos2(a) – 1 = cos2 (a) – sin2 (a)

tan 2a = 2 tana / (1 – tan2 (a))

Công thức nhân 3

sin3a = 3sina – 4sin3 (a)

cos 3a = 4cos3 (a) – 3 cos (a)

tan 3a = (3tan a – tan3 (a)) / (1 – 3tan2 (a))

Công thức hạ bậc

sin2 (a) = (1 – cos 2a) / 2

cos2 (a) = (1 + cos 2a) / 2

sin3 (a) = (3sina – sin 3a) / 4

cos3 (a) = (3cosa + cos 3a) / 4

Các công thức lượng giác đặc biệt trong các cung liên quan đặc biệt

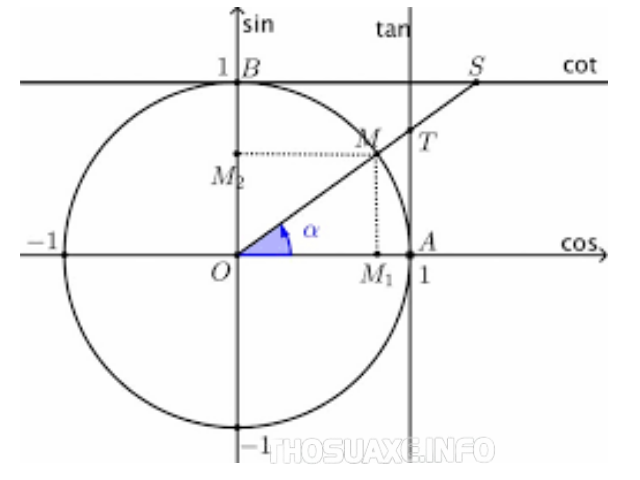
Công thức tính lượng giác trong các cung đặc biệt

• Hai cung đối nhau (α và – α)

sinα = – sin (-α)

cosα = cos (-α)

tanα = – tan (-α)

cotα = – cot (-α)

• Hai cung bù nhau ( α và π – α)

sinα = sin (π – α)

cosα = – cos (π – α)

tanα = – tan (π – α)

cotα = – cot (π – α)

• Hai cung phụ nhau – tổng hai góc bằng 90 độ (α và π/2 – α)

sinα = cos (π/2 – α)

cosα = sin (π/2 – α)

tanα = cot (π/2 – α)

cotα = tan (π/2 – α)

• Hai cung lệch π (α và π + α)

sinα = – sin (π + α)

cosα = – cos (π + α)

tanα = tan (π + α)

cotα = cot (π + α)

• Hai cung lệch π/2 (α và π/2 + α)

sinα = cos (π/2 + α)

cosα = – sin (π/2 + α)

Mẹo ghi nhớ của các công thức phức tạp đặc biệt này là cos đối – sin bù – phụ chéo – lệch π tan cot.

Trên đây chúng tôi vừa tổng hợp lại các công thức lượng giác cơ bản và nâng cao phổ biến. Hy vọng bài viết này sẽ giúp bạn có thêm kiến thức về lượng giác để phục vụ cho công việc học tập của mình. Chúc các bạn ghi nhớ các công thức toán học này thành công nhé.

Xem thêm:

Giải đáp Toán học: Tổ hợp, chỉnh hợp, hoán vị là gì?

Số thập phân là gì? Hướng dẫn cộng, trừ, nhân, chia số thập phân

Số chính phương là gì? Đặc điểm và một số bài toán ví dụ