Contents
Sự ra đời của định lý hàm Cos (còn gọi là định lý Cosin)
Định lý hàm Cos của Al Kashi
Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Ông đồng thời là nhà thiên văn học nổi tiếng vùng Trung Á, một trong các nhà bác học lớn của trường phái Samarkand đầu thế kỷ XV ít ỏi còn lại.
Nhắc đến định lý Cosin của ông, người ta còn gọi là định lý Al Kashi.
Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:
- Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó
- Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết

Định lý Cosin của Euclide
Bên cạnh phát minh chính thức về hàm Cosin, có một phát biểu toán học được cho là tương đương định lý hàm số Cosin. Nó được đưa ra bởi nhà toán học Euclide, vào thế kỷ thứ III trước công nguyên.
Nội dung: “Trong một tam giác tù, bình phương của cạnh đối diện góc tù lớn hơn tổng bình phương của của hai cạnh kề góc tù là hai lần diện tích của hình chữ nhật bao gồm một cạnh bằng một trong hai cạnh kề góc tù của tam giác (cạnh có đường cao hạ xuống nó) và đoạn thẳng đã được cắt giảm từ đường thẳng kéo dài của cạnh đó về phía góc tù bởi đường cao trên.”
Định lý hàm Cos trong tam giác
Hai nội dung định lý hàm Cos trong tam giác (lượng giác) với định lý hàm Cos trong Vật Lý không giống nhau, hãy xem hết nội dung để nắm rõ hơn.
Định định lý Cosin trong hình học Eculid biểu diễn mối liên quan giữa chiều dài các cạnh của một tam giác (trong mặt phẳng) với Cosin (hay cos) của góc tương ứng.
Phát biểu và công thức định lý cosin
Phát biểu định lý Cosin: “Ở trong một tam giác phẳng, bình phương một cạnh bằng tổng bình phương hai cạnh còn lại trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó”.
Công thức: Cho một tam giác phẳng ABC bất kì có độ dài các cạnh lần lượt như sau: BC = a, AC = b, AB = c, gọi các góc tương ứng: góc A = alpha, góc B = beta, góc C = gamma, ta có:
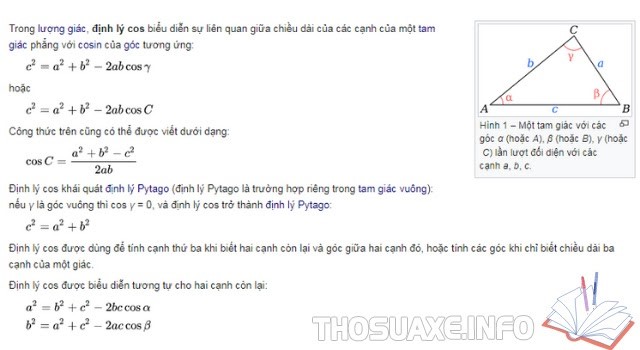
Nhận xét: Xét trong mặt phẳng, nếu có 1 tam giác biết trước hai cạnh và góc xen giữa, ta sẽ tính được độ dài của cạnh còn lại hoặc có thể tính góc khi biết 3 cạnh của tam giác đó.
Ta dễ dàng thấy được, nội dung định lý Pytago là trường hợp đặc biệt của định lý Cosin, cụ thể:
Cho tam giác ABC là tam giác vuông, ta suy ra được:
- Khi tam giác ABC vuông tại A, cos α (hoặc A) = 0 => a2 = b2 + c2
- Khi tam giác ABC vuông tại B, cos β (hoặc B) = 0 => b2 = a2 + c2
- Khi tam giác ABC vuông tại C, cos γ (hoặc C) = 0 => c2 = a2 + b2
Chứng minh định lý Cosin
Có rất nhiều cách để chứng minh định lý Cosin là đúng, tiêu biểu như:
– Sử dụng công thức tính khoảng cách (dùng được cho cả tam giác nhọn và tam giác tù):

– Dựa vào công thức lượng giác

– Áp dụng định lý Pytago (trường hợp tam giác tù):

– Áp dụng định lý Pytago (trường hợp tam giác nhọn):

– Áp dụng định lý Ptolemy

Hệ quả của định lý hàm Cos
Ứng dụng của định lý Cosin trong giải bài tập liên quan đến giải tam giác hoặc một đường tròn:
- Xác định cạnh thứ ba của một tam giác khi biết 2 cạnh còn lại và góc xen giữa
- Tìm ba góc khi đã biết 3 cạnh của một tam giác
- Tìm cạnh thứ ba khi biết hai cạnh còn lại và góc đối diện một trong hai cạnh cho trước

Trong đó, công thức số 3 trong hình có được nhờ giải phương trình bậc hai a2 − 2ab cos γ + b2 − c2 = 0 (a là ẩn) (I).
Phương trình (I) có nghiệm như sau:
- (I) có hai nghiệm dương nếu b sin γ < c < b
- (I) có 1 nghiệm dương duy nhất nếu c ≥ b hoặc c = b sin γ
- (I) có vô nghiệm nếu c < b sin γ
Những chia sẻ về chủ đề Định lý hàm Cos trong tam giác vừa rồi mong rằng sẽ giúp các bạn hiểu rõ và toàn diện hơn về kiến thức này. Từ đó, áp dụng giải tốt các bài toán liên quan!
Xem thêm:
- Định lý Vi-et – các dạng bài ứng dụng định lý Vi-et quan trọng
- Hiệu suất là gì? Làm sao để đẩy được hiệu suất làm việc lên cao?
- Số nguyên là gì? Phân loại, tính chất và cách biểu diễn trên trục số
- Tích phân là gì? Các công thức tính tích phân mà bạn nên biết
- Công thức tính chu vi – diện tích hình chữ nhật và ví dụ chi tiết