Contents
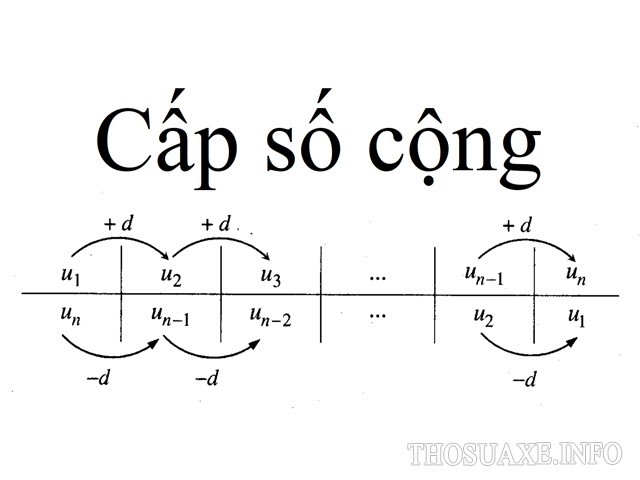
Cấp số cộng là gì?
Cấp số cộng là một khái niệm toán học cơ bản được sử dụng để chỉ một dãy số (có thể hữu hạn hoặc vô hạn) thỏa mãn điều kiện hai phần tử liên tiếp trong dãy sai khác nhau giá trị tương ứng với một hàng số nhất định. Hằng số sai khác của dãy được gọi là công sai của cấp số cộng. Các phần tử của dãy được gọi là các số hạng.

Ví dụ:
1, 3, 5, 7, 9, … là một cấp số cộng với công sai là 2 và các số hạng là 1, 3, 5, 7, …
1, 5, 9, 13, … là một cấp số cộng với công sai là 4 và 4 và các số hạng là 1, 5, 9, 13, …
Số hạng tổng quát của Cấp số cộng
Đối với cấp số cộng có số hạng đầu tiên là a1 và công sai là hằng số d, ta có thể trình bày số hạng thứ n trong cấp số ở dạng tổng quát như sau:
an=a1+(n-1)d
Tổng của một Cấp số cộng
Cấp số cộng có thể là một dãy số hữu hạn hoặc vô hạn. Đối với cấp số vô hạn thì việc tính toán tổng của các số hạng là điều không thể. Tuy nhiên nếu đó là một cấp số hữu hạn mà ta biết được số hạng đầu, số hạng cuối cùng công sai, việc tính toán tổng của cấp số cộng này lại vô cùng đơn giản. Ta sẽ không phải tính tổng từng số hạng riêng lẻ mà chỉ cần áp dụng công thức tính tổng quát được chứng minh bởi nhà Toán học Carl Friedrich Gauss.
Công thức này được trình bày như sau:
Sn=a1+a2+…+an=n(a1 + an)2=n[2a1 + (n-1)d]2
Trong đó:
Sn là tổng của cấp số cộng
a1, a2, … , an là các số hạng của cấp số cộng
d là công sai của cấp số cộng
n là số lượng số hạng của cấp số
Ví dụ:
Cho cấp số cộng: 1, 3, 5, … 99 yêu cầu tính tổng của cấp số cộng này.
Trước hết chúng ta có thể xác nhận được công sai của cấp số cộng này là 2 và số lượng số hạng của cấp số này là 49.
Áp dụng công thức ta tính được tổng của cấp số cộng này là:
S=49(1+99)2=49.1002=49002=2450
Tích của một Cấp số cộng
Đối với một cấp số cộng hữu hạn có số hạng đầu là a1 và công sai d và n số hạng, ta có thể tính được tích của cấp số cộng này bằng công thức sau:
a1.a2…..an=a1(a1+d)(a1+2d)…[a1+(n-1)d]
=d n(a1d)(a1d+1)(a1d+2)…[a1d+(n-1)]
=d n(a1d)n
=d n(a1d+n)(a1d)

Trong đó: xnlà giai thừa trên có giá trị được biểu thị bằng biểu thức dưới đây:
xn=x(x+1)(x+2)…(x+n-1) =(x+n-1)!(x-1)!
là ký hiệu của hàm gamma có giá trị được thể hiện dưới đây:
(z)=0t z-1e-tdt
Ví dụ:
Cho cấp số cộng: 1, 3, 5,… 99 yêu cầu tính tích của cấp số cộng này.
Trước hết chúng ta có thể xác nhận được công sai của cấp số cộng này là 2 và số lượng số hạng của cấp số này là 49.
Áp dụng công thức ta tính được tích của cấp số cộng này là:
=249(12)49
=249(12+49-1)!(12-1)!
=249.97!
=57,031.10165
Hy vọng bài viết trên đây của chúng tôi đã giúp bạn hiểu thêm về cấp số cộng là gì và cách ứng dụng khái niệm toán học này trong giải bài tập cũng như đời sống. Đừng quên thường xuyên truy cập website của chúng tôi để cập nhật thêm những kiến thức toán học mới nhé!
Xem thêm: